Équation diophantienne ax + by = c

L'équation ax by = c, où les coefficients a, b et c sont trois entiers relatifs (a et b non tous deux nuls) et où les inconnues x et y sont des entiers relatifs, est une des équations diophantiennes les plus simples à résoudre. Sa résolution s'appuie sur l'algorithme d'Euclide, le théorème de Bachet-Bézout (qui correspond au cas, appelé aussi identité de Bézout, où c est égal au PGCD de a et b) et le théorème de Gauss.

Dans l'ensemble des entiers relatifs, une telle équation possède, ou bien aucune solution, ou bien une infinité de solutions. Lorsque les coefficients et les inconnues sont des entiers naturels, l'équation possède un nombre fini de solutions. Le théorème de Paoli en donne le nombre à 1 près.

Recherche de solutions dans l'ensemble des entiers relatifs

Équation ax by = 1 où a et b sont premiers entre eux

Le théorème de Bachet-Bézout affirme que cette équation admet toujours au moins une solution.

La première étape de la résolution consiste à trouver une solution particulière, c'est-à-dire un couple d'entiers relatifs (x₀, y₀) vérifiant : ax₀ by₀ = 1.

• L'algorithme d'Euclide étendu permet d'en exhiber une. (On peut remarquer que cet algorithme s'interprète comme le calcul du développement en fraction continue du rationnel a/b ; l'avant dernière réduite h_n–1/k_n–1 fournit une solution du problème, puisque k_n–1a – h_n–1b = (–1)^{n 1}.)
• On peut travailler modulo b, en cherchant d'abord un entier x₀ tel que ax₀ ≡ 1 (mod b). L'entier y₀ se calcule ensuite comme étant égal à (1 – ax₀)/b.
  • Pour trouver un x₀ inverse de a mod b, on peut se servir du théorème de Fermat généralisé par Euler, d'après lequel a^φ(b) est congru à 1 modulo b, où φ est l'indicatrice d'Euler : l'entier x₀ = a^φ(b)–1 convient. De même, l'entier x₀ = a^λ(b)–1 convient, où λ est la fonction de Carmichael.
  • Mais on peut aussi, si b n'est pas trop grand, chercher une solution par simple balayage, en cherchant quel entier x₀ compris entre 1 et |b| – 1 vérifie la congruence linéaire ax₀ ≡ 1 (mod b).

En effet, il est facile de vérifier qu'un tel couple est solution du problème :

${\displaystyle \forall k\in \mathbb {Z} ,\,a(x_{0} bk) b(y_{0}-ak)=ax_{0} by_{0}=1.}$

Il s'agit maintenant de prouver que seuls ces couples sont solutions. Supposons donc que le couple (x, y) est solution de l'équation. On a donc

${\displaystyle (1):\qquad ax by=1=ax_{0} by_{0}.}$

En regroupant autrement les termes, on obtient

${\displaystyle (2):\qquad a(x-x_{0})=-b(y-y_{0}).}$

L'entier b divise donc le produit a(x – x₀). Comme a et b sont premiers entre eux, le lemme de Gauss permet de dire que b divise x – x₀. Il existe donc un entier relatif k tel que x – x₀ = kb. Soit encore

${\displaystyle (3):\qquad x=x_{0} kb.}$

En remplaçant x – x₀ par kb dans (2), on obtient :

${\displaystyle (4)\qquad akb=-b(y-y_{0}).}$

Puis en simplifiant par –b

${\displaystyle (5)\qquad y-y_{0}=-ak.}$

Soit encore

${\displaystyle (6)\qquad y=y_{0}-ak.}$

Donc, si (x, y) est solution de (1) alors, il existe un entier relatif k tel que (x, y) = (x₀ bk, y₀ – ak).

Équation ax by = c où a et b sont premiers entre eux

Une solution particulière peut être trouvée en multipliant par c une solution particulière de l'équation ax by = 1. En effet, si (x₀, y₀) vérifie ax₀ by₀ = 1 alors ax₀c by₀c = c ; le couple (x₀c, y₀c) est alors solution de l'équation ax by = c.

Un raisonnement analogue au précédent permet de trouver l'ensemble des solutions :

Cas général

On appelle d le pgcd de a et de b.

En effet, d divisant a et b, d divise aussi toute expression de la forme ax by où x et y sont des entiers relatifs, donc d doit diviser c.

On suppose maintenant que d divise c ; il existe alors trois entiers relatifs a₁, b₁ et c₁ tels que

a = da₁

b = db₁

c = dc₁

avec a₁ et b₁ premiers entre eux.

L'équation ax by = c est alors équivalente à l'équation a₁x b₁y = c₁ dans laquelle a₁ et b₁ sont premiers entre eux, et ce cas a déjà été résolu. On obtient alors la résolution dans le cas général :

Une solution particulière (x₁, y₁) étant connue, l'ensemble des solutions est formé des couples (x₁ b₁k, y₁ – a₁k) où k est un entier relatif quelconque.

D'où la propriété :

Système minimal

On suppose dans cette section que c est un multiple de d. Parmi toutes les solutions d'une équation ax by = c donnée, on peut chercher celle(s) pour laquelle x² y² soit la plus petite possible.

Il s'agit de rendre minimale la valeur (x₁ b₁k)² (y₁ – a₁k)². Si l'on considère la fonction de la variable réelle t définie par f(t) = (x₁ b₁t)² (y₁ – a₁t)², l'étude de cette fonction du second degré montre que celle-ci possède un minimum en ${\displaystyle t={\frac {a_{1}y_{1}-b_{1}x_{1}}{a_{1}^{2} b_{1}^{2}}}.}$ Si t est entier, le couple solution est alors (x₁ b₁t, y₁ – a₁t) ; sinon, l'entier qui rend f minimale est le (ou les) entier(s) k le(s) plus proche(s) de t.

Le(s) couple(s) d'entiers solution de ax by = c dont la valeur x² y² est minimale est (ou sont) le (ou les) couple(s) (x₁ b₁k, y₁ – a₁k) où k est le (ou les) entier(s) le(s) plus proche(s) de t = (a₁y₁ – b₁x₁)/(a₁² b₁²).

Dans le cas où a et b sont premiers entre eux, le cas où t est entier mérite d'être explicité. On démontre que t est entier si et seulement si l'entier c est un multiple de a² b². La solution du système minimal est alors ${\displaystyle \left({\frac {ac}{a^{2} b^{2}}},{\frac {bc}{a^{2} b^{2}}}\right)}$.

Dans le cas où a et b sont premiers entre eux, il existe deux solutions au système minimal si et seulement si a et b sont impairs et l'entier c est un multiple impair de (a² b²)/2.

Applications

Congruence

La résolution de l'équation ax by = 1, où a et b sont premiers entre eux, permet de trouver un inverse à a modulo b, c'est-à-dire un entier x tel que ax ≡ 1 (mod b). L'ensemble des solutions permet de dire qu'il existe une unique classe x telle que ax = 1 dans ℤ/bℤ. En effet, parmi les couples solutions, tous les entiers x sont congrus modulo b.

Équation de droite

L'ensemble des points M(x, y) vérifiant l'équation ax by = c forme une droite. Les couples d'entiers relatifs vérifiant cette équation correspondent aux points M de la droite dont les coordonnées sont entières. La résolution de l'équation dans l'ensemble des entiers relatifs permet de donner les coordonnées de ces points. Selon la valeur de c, la droite D peut ne jamais passer par des points de coordonnées entières ou bien posséder une infinité de points de coordonnées entière régulièrement répartis.

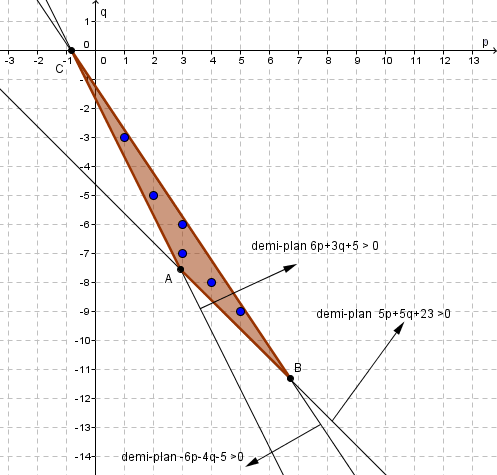
La solution du système minimal se lit alors très facilement. Le ou les couples solutions correspondent aux points dont les coordonnées vérifient x² y² est minimal. Ce sont donc les points de la droite les plus proches de l'origine. Le point O se projette sur la droite en H. La solution du système minimal est donc le (ou les) points de la droite de coordonnées entières situé(s) le plus près de H.

Réduction d'une fraction en éléments simples

Décomposer une fraction irréductible A/B en éléments simples, c'est la décomposer en somme d'un entier relatif et de fractions de la forme r_j,i / p_i ^j dans laquelle p_i est un nombre premier apparaissant dans la décomposition de B en facteurs premiers, j est un exposant entier non nul ne dépassant pas l'exposant de p_i dans la décomposition de B et r_j,i est un entier compris entre 0 et p_i – 1.

Lucas prouve l'existence d'une telle décomposition. Il procède en plusieurs étapes.

Si ${\displaystyle B=p^{n}}$, où p est un nombre premier, une simple écriture de A dans la base p permet d'aboutir. En effet

${\displaystyle A=r_{0} r_{1}p r_{2}p^{2} \cdots r_{n-1}p^{n-1} Ep^{n}}$

où les ${\displaystyle r_{i}}$ sont des entiers compris entre 0 et p – 1 et E est un entier relatif. D'où en divisant par B

${\displaystyle {\frac {A}{B}}={\frac {r_{0}}{p^{n}}} {\frac {r_{1}}{p^{n-1}}} \cdots {\frac {r_{n-1}}{p}} E.}$

La seconde étape consiste à travailler sur un nombre B = ab où a et b sont premiers entre eux et c'est là qu'intervient l'équation diophantienne. Les deux nombres sont premiers entre eux, il existe donc des entiers relatifs x et y tels que

ax by = A

donc

${\displaystyle {\frac {A}{B}}={\frac {A}{ab}}={\frac {x}{b}} {\frac {y}{a}}.}$

La décomposition de la fraction sera donc établie dès que seront obtenues les décompositions des fractions x/b et y/a.

Lucas procède alors de proche en proche. Si ${\displaystyle B=p_{1}^{n_{1}}\times p_{2}^{n_{2}}\times \cdots \times p_{k}^{n_{k}}}$ alors on peut poser ${\displaystyle a=p_{1}^{n_{1}}}$ et ${\displaystyle b={\frac {B}{a}}}$

${\displaystyle {\frac {A}{B}}={\frac {A}{ab}}={\frac {x}{b}} {\frac {y}{a}}={\frac {x}{b}} {\frac {y}{p_{1}^{n_{1}}}}.}$

La seconde fraction se décompose aisément et la première est à décomposer en utilisant le même processus. Il suffit de k – 1 étapes pour arriver au bout de la décomposition complète.

Lucas démontre que malgré la multiplicité des méthodes pour arriver à la décomposition, celle-ci est unique.

Exemple : Décomposition de la fraction ${\displaystyle {\frac {259}{90}}}$

On décompose 90 en 9×10. On cherche deux entiers x et y tels que 9x 10y = 259. On peut prendre x = 1 et y = 25.

${\displaystyle (1)\qquad {\frac {259}{90}}={\frac {1}{10}} {\frac {25}{9}}.}$

On décompose 10 en 2×5. On cherche deux entiers x et y tels que 2x 5y = 1. On peut prendre x = 3 et y = –1.

${\displaystyle (2)\qquad {\dfrac {1}{10}}={\dfrac {3}{5}}-{\dfrac {1}{2}}=-1 {\dfrac {3}{5}} {\dfrac {1}{2}}.}$

On écrit 25 en base 3

${\displaystyle \qquad 25=1 3\times 8=1 3\times (2 3\times 2)=1 2\times 3 2\times 3^{2}.}$

Donc

${\displaystyle (3)\qquad {\frac {25}{9}}={\frac {1}{3^{2}}} {\dfrac {2}{3}} 2.}$

Il suffit de remplacer dans (1) les résultats trouvés dans (2) et (3)

${\displaystyle {\frac {259}{90}}=1 {\frac {1}{3^{2}}} {\dfrac {2}{3}} {\dfrac {3}{5}} {\dfrac {1}{2}}.}$

Généralisation aux dimensions supérieures

Les techniques mises en place pour la résolution de l'équation ax by = c peuvent être réinvesties pour la résolution des équations linéaires à plus d'inconnues. En particulier, elles permettent de résoudre l'équation diophantienne linéaire ax by cz = d.

Comme dans le cas de la dimension 2, on peut remarquer que l'équation n'admet pas de solution si d n'est pas un multiple du PGCD de (a, b, c). Si d est multiple du PGCD, on peut diviser chacun des coefficients par le PGCD, on se ramène alors à une équation du même type dans lequel les coefficients devant x, y et z sont premiers entre eux dans leur ensemble.

Dans l'équation ax by cz = d, où a, b, c sont premiers entre eux, on pose b∧c le PGCD de b et c et note b₁ et c₁ les entiers relatifs premiers entre eux tels que

${\displaystyle b=b_{1}.b\wedge c}$

${\displaystyle c=c_{1}.b\wedge c}$

by cz étant toujours un multiple de b∧c, l'équation est équivalente au système

${\displaystyle {\begin{cases}(1)\qquad by cz=(b\wedge c)Y\\(2)\qquad ax (b\wedge c)Y=d.\end{cases}}}$

Les entiers a et b∧c étant premiers entre eux, la seconde équation admet des solutions et, pour tout Y la première équation admet des solutions. L'équation ax by cz = d admet donc toujours des solutions.

On appelle (x₁, y₁, z₁) l'une d'entre elles et (y₀, z₀) une solution de l'équation b₁y c₁z = 1. On peut noter by₁ cz₁ = (b∧c)Y₁.

Les solutions de l'équation (2) sont les couples : ${\displaystyle (x_{1} (b\wedge c)k,Y_{1}-ak)}$ où k est un entier relatif quelconque.

L'équation (1) s'écrit alors :

${\displaystyle by cz=by_{1} cz_{1}-a(b\wedge c)k\Leftrightarrow b_{1}(y-y_{1}) c_{1}(z-z_{1})=-ak}$

dont les solutions sont les couples :

${\displaystyle (y_{1}-aky_{0} c_{1}h,z_{1}-akz_{0}-b_{1}h)\,}$

où h est un entier relatif quelconque.

Les solutions de l'équation de départ sont donc données par l'égalité matricielle suivante

${\displaystyle {\begin{pmatrix}x\\y\\z\end{pmatrix}}={\begin{pmatrix}x_{1}\\y_{1}\\z_{1}\end{pmatrix}} {\begin{pmatrix}b\wedge c&0\\-ay_{0}&c_{1}\\-az_{0}&-b_{1}\end{pmatrix}}{\begin{pmatrix}k\\h\end{pmatrix}}}$

où h et k sont des entiers relatifs quelconques.

Recherche de solutions dans l'ensemble des entiers naturels

On ne considère ici que la résolution de l'équation ax by = c où a, b, c sont des entiers naturels, a et b non nuls et premiers entre eux, les solutions étant cherchées parmi les entiers naturels.

Lucas attribue à Petri Paoli et Ernesto Cesàro les deux résultats suivants :

Si l'on s'intéresse alors plus précisément aux entiers r compris entre 0 et ab – 1 pour lesquels l'équation ax by = r admet une solution, on peut démontrer que :

• si r est multiple de a ou de b, l'équation comporte une unique solution ;
• parmi les deux équations ax by = r et ax by = ab – r où r n'est multiple ni de a ni de b, une exactement a une solution entière positive ;
• si r est inférieur à a b et n'est multiple ni de a ni de b, l'équation ne comporte pas de solution.

On déduit de ces trois points que le plus grand entier r pour lequel l'équation ax by = r n'a pas de solution positive (appelé le nombre de Frobenius de {a, b}) est égal à ab – a – b.

Des deux premiers points, on déduit le théorème suivant :

Lorsqu'un entier r compris entre 1 et ab – 1 est donné, pour déterminer si l'équation ax by = r admet une solution, il faut observer le système minimal. Le point de la droite ax by = r le plus proche de l'origine est de coordonnées rationnelles positives.

L'unique solution entière positive (si elle existe) de l'équation ax by = r correspond à un des points de la droite à coordonnées entières les plus proches de ce point. Si (x₁, y₁) est une solution dans l'ensemble des entiers relatifs de l'équation ax by = r, l'unique solution positive (si elle existe) de l'équation est donc à chercher dans les deux couples (x₁ bk₁, y₁ – ak₁) ou (x₁ bk₂, y₁ – ak₂) où k₁ et k₂ sont les deux entiers les plus proches de (ay₁ – bx₁)/(a² b²). Si aucun de ces deux couples n'est dans ℕ², l'équation n'admet pas de solution.

Notes et références

Liens externes

• (en) Eric W. Weisstein, « Diophantine Equation », sur MathWorld

• Arithmétique et théorie des nombres